oktober 12th, 2010
Toril Johannessen
Variable Stars, 2009


At the beginning of the 20th century the estimated size of the universe increased radically.
At that time, an extensive project of photographing and mapping the entire starry sky took place at Harvard College Observatory, Cambridge, MA, where catalogue work and mathematical calculations were carried out by a group of women known as The Harvard Computers.
With the introduction of photography to astronomy, the amount of scientific data processed at Harvard College Observatory became immense. Women were considered as accurate and cheap labor to perform the work, and although they had no status as scientific staff, several of them developed theories founded on the work they did. One of these theories was a method to calculate distances in space based on observations of variable stars; stars that vary in brightness over a period of time. Henrietta Swan Leavitt, who worked on classification of such stars at the observatory, found a correlation between brightness and period of a particular type of variable stars. Building on her discovery, new theories on the scale and expansion of the universe were introduced, and the scale of the universe as we know it increased by billions of light years.
…
The work Variable Stars takes Harvard College Observatory’s grand archive of photographic plates as its very tangible vantage point. With the task to collect a sequence of stars visible from her location in Norway, the artist travelled to Cambridge and dug into the archive of photographic plates.
The photographs presented in the installation Variable Stars are printed copies of glass plates taken at Harvard College Observatory, originally taken for Northern catalogue work and for the study of variable stars. They show sections of the sky that are in viewing angle from the window after sunset in the gallery room where the installation were firstly exhibited in Oslo Kunstforening, Oslo, Norway, January 17th 2009.
In each photograph one cepheid or RR Lyrae star is located; two types of variable stars that are used for distance measurements. The stars are cut from the photographic copies and then used as seeds for growing crystals of alum, a substance that is used as a component in photographic paper. The installation on view at Oslo Kunstforening contained of 17 photographs and the corresponding crystals, telescopes at the window and a triptych of pencil drawings.
The Scale of The Universe The Past 100 Years, 2009
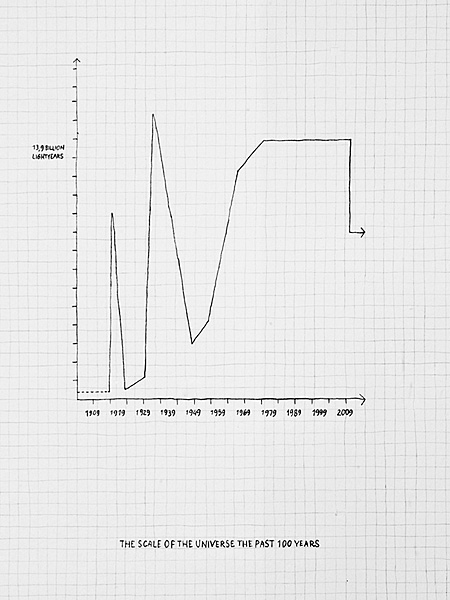
We shall never understand it until we find a way to send up a net and fetch the thing down (Henrietta Swan Leavitt)
Posted in Cosmology, Mathematics, Visual Arts | Reacties uitgeschakeld voor The Scale of The Universe
februari 19th, 2006
The Three Body Problem is the mathematical problem of finding the positions and velocities of three massive bodies, which are interacting each other gravitationally, at any point in the future or the past, given their present positions, masses, and velocities. An example would be to completely solve the behavior of the Sun-Jupiter-Saturn system, or that of three mutually orbiting stars. It is a vastly more difficult exercise than the two-body problem. In fact, as Henri Poincaré (1854-1912) and others showed, the three-body problem is impossible to solve in the general case; that is, given three bodies in a random configuration, the resulting motion nearly always turns out to be chaotic: no one can predict precisely what paths those bodies would follow.
Watch here: The Tree Body Problem animation
Genetologic Research Nr. 6, 2003 (300cm x 300cm x 300cm)


Maarten Vanden Eynde
Three wooden (oak) beams are manually bended by fire and water during a three week lasting ’torture-session’. After being liberated from the bending-machine, the beams stay in their forced position. The thee bodies are photographed in a certain way, but can change position without loosing their inter-relating balance. Various positions have been tried and just a few points of view bring them into a harmonious equilibrium. Any change or random elaboration creates chaos or disharmony.
Posted in Mathematics, Pyrography, Visual Arts | Reacties uitgeschakeld voor The Three Body Problem
februari 10th, 2006
The Universal Law of Gravitation has several important features. First, it is an inverse square law, meaning that the strength of the force between two massive objects decreases in proportion to the square of the distance between them as they move farther apart. Second, the direction in which the force acts is always along the line (or vector) connecting the two gravitating objects.
In 1687 Sir Isaac Newton first published his Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) which was a radical treatment of mechanics, establishing the concepts which were to dominate physics for the next two hundred years. Among the book’s most important new concepts was Newton’s Universal Law of Gravitation. Newton managed to take Kepler’s Laws governing the motion of the planets and Galileo’s ideas about kinematics and projectile motion and synthesize them into a law which governed both motion on earth and motion in the heavens. This was an achievement of enormous importance for physics; Newton’s discoveries meant that the universe was a rational place in which the same principles of nature applied to all objects.
Maarten Vanden Eynde
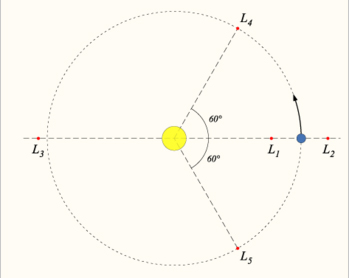
‘Between two objects, let’s say A and B, there is a point where the gravitation of both objects is working with equal force (L1 point, named after Lagrange). This point is balancing between the two attracting masses. If it is slightly bending towards A or B is will be attracted more by either one of them. It can only move from it’s frozen position, without loosing it’s equal balance, if A and B change mass simultaneously. The mass A is loosing, B has to gain.
Time is always moving. When you read this word, it became history already. The future is catching up instantly. The present is an untouchable point always on the move.
If time would be a linear experience, and A would be the past and B the future, than the point hanging in the middle would be the present. The past is getting longer and longer (or bigger and bigger) so in order for this point to be equally drawn to both A and B, it needs to be moving towards the future. The past is getting bigger and the future is getting smaller. And on top of that the speed of this process is accelerating. Just like the birth of matter during the big bang, time was created at the same time and moves equally with the expanding universe; faster and faster to it’s final destiny. Will this be the end or a new beginning?’

The Lagrangian points (also Lagrange point, L-point, or libration point), are the five positions in interplanetary space where a small object affected only by gravity can theoretically be stationary relative to two larger objects (such as a satellite with respect to the Earth and Moon). They are analogous to geosynchronous orbits in that they allow an object to be in a “fixed” position in space rather than an orbit in which its relative position changes continuously.
Read the rest of this entry »
Posted in Barology, Horology, Mathematics, Philosophy | Reacties uitgeschakeld voor Gravitation of Time






