Gravitation of Time
The Universal Law of Gravitation has several important features. First, it is an inverse square law, meaning that the strength of the force between two massive objects decreases in proportion to the square of the distance between them as they move farther apart. Second, the direction in which the force acts is always along the line (or vector) connecting the two gravitating objects.
In 1687 Sir Isaac Newton first published his Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) which was a radical treatment of mechanics, establishing the concepts which were to dominate physics for the next two hundred years. Among the book’s most important new concepts was Newton’s Universal Law of Gravitation. Newton managed to take Kepler’s Laws governing the motion of the planets and Galileo’s ideas about kinematics and projectile motion and synthesize them into a law which governed both motion on earth and motion in the heavens. This was an achievement of enormous importance for physics; Newton’s discoveries meant that the universe was a rational place in which the same principles of nature applied to all objects.
Maarten Vanden Eynde
‘Between two objects, let’s say A and B, there is a point where the gravitation of both objects is working with equal force (L1 point, named after Lagrange). This point is balancing between the two attracting masses. If it is slightly bending towards A or B is will be attracted more by either one of them. It can only move from it’s frozen position, without loosing it’s equal balance, if A and B change mass simultaneously. The mass A is loosing, B has to gain.
Time is always moving. When you read this word, it became history already. The future is catching up instantly. The present is an untouchable point always on the move.
If time would be a linear experience, and A would be the past and B the future, than the point hanging in the middle would be the present. The past is getting longer and longer (or bigger and bigger) so in order for this point to be equally drawn to both A and B, it needs to be moving towards the future. The past is getting bigger and the future is getting smaller. And on top of that the speed of this process is accelerating. Just like the birth of matter during the big bang, time was created at the same time and moves equally with the expanding universe; faster and faster to it’s final destiny. Will this be the end or a new beginning?’

The Lagrangian points (also Lagrange point, L-point, or libration point), are the five positions in interplanetary space where a small object affected only by gravity can theoretically be stationary relative to two larger objects (such as a satellite with respect to the Earth and Moon). They are analogous to geosynchronous orbits in that they allow an object to be in a “fixed” position in space rather than an orbit in which its relative position changes continuously.
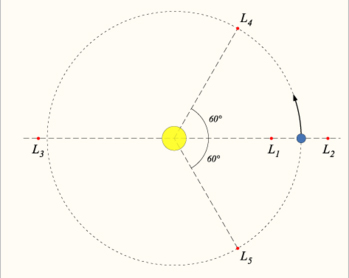
A more precise but technical definition is that the Lagrangian points are the stationary solutions of the circular restricted three-body problem. For example, given two massive bodies in circular orbits around their common center of mass, there are five positions in space where a third body, of comparatively negligible mass, could be placed which would then maintain its position relative to the two massive bodies. As seen in a frame of reference which rotates with the same period as the two co-orbiting bodies, the gravitational fields of two massive bodies combined with the centrifugal force are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies.
The five Lagrangian points are labeled and defined as follows:
L1
The L1 point lies on the line defined by the two large masses M1 and M2, and between them.
Example: An object which orbits the Sun more closely than the Earth would normally have a shorter orbital period than the Earth, but that ignores the effect of the Earth’s own gravitational pull. If the object is directly between the Earth and the Sun, then the effect of the Earth’s gravity is to weaken the force pulling the object towards the Sun, and therefore increase the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the L1 point, the orbital period of the object becomes exactly equal to the Earth’s orbital period.
The Sun–Earth L1 is ideal for making observations of the Sun. Objects here are never shadowed by the Earth or the Moon. The Solar and Heliospheric Observatory (SOHO) is stationed in a Halo orbit at the L1 and the Advanced Composition Explorer (ACE) is in a Lissajous orbit, also at the L1 point. The Earth–Moon L1 allows easy access to lunar and earth orbits with minimal delta-v, and would be ideal for a half-way manned space station intended to help transport cargo and personnel to the Moon and back.
L2
The L2 point lies on the line defined by the two large masses, beyond the smaller of the two.
Example: On the side of the Earth away from the Sun, the orbital period of an object would normally be greater than that of the Earth. The extra pull of the Earth’s gravity decreases the orbital period of the object, and at the L2 point that orbital period becomes equal to the Earth’s.
Sun–Earth L2 is a good spot for space-based observatories. Because an object around L2 will maintain the same orientation with respect to the Sun and Earth, shielding and calibration are much simpler. The Wilkinson Microwave Anisotropy Probe is already in orbit around the Sun–Earth L2. The future Herschel Space Observatory as well as the proposed James Webb Space Telescope will be placed at the Sun–Earth L2. Earth–Moon L2 would be a good location for a communications satellite covering the Moon’s far side.
If M2 is much smaller than M1, then L1 and L2 are at approximately equal distances r from M2, equal to the radius of the Hill sphere, given by:
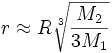
where R is the distance between the two bodies.
This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by 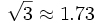
Examples:
Sun and Earth: 1,500,000 km from the Earth
Earth and Moon: 61,500 km from the Moon
L3
The L3 point lies on the line defined by the two large masses, beyond the larger of the two.
Example: L3 in the Sun–Earth system exists on the opposite side of the Sun, a little further away from the Sun than the Earth is, where the combined pull of the Earth and Sun again causes the object to orbit with the same period as the Earth. The Sun–Earth L3 point was a popular place to put a “Counter-Earth” in pulp science fiction and comic books.
L4 and L5
The L4 and L5 points lie at the third point of an equilateral triangle with the base of the line defined by the two masses, such that the point is ahead of, or behind, the smaller mass in its orbit around the larger mass.
L4 and L5 are sometimes called triangular Lagrange points or Trojan points.
Examples: The Sun–Earth L4 and L5 points lie 60° ahead of and 60° behind the Earth in its orbit around the Sun. They contain interplanetary dust. The Sun–Jupiter L4 and L5 points are occupied by the Trojan asteroids.
Stability
The first three Lagrangian points are technically stable only in the plane perpendicular to the line between the two bodies. This can be seen most easily by considering the L1 point. A test mass displaced perpendicularly from the central line would feel a force pulling it back towards the equilibrium point. This is because the lateral components of the two masses’ gravity would add to produce this force, whereas the components along the axis between them would balance out. However, if an object located at the L1 point drifted closer to one of the masses, the gravitational attraction it felt from that mass would be greater, and it would be pulled closer. (The pattern is very similar to that of tidal forces.)
Although the L1, L2, and L3 points are nominally unstable, it turns out that it is possible to find stable periodic orbits around these points, at least in the restricted three-body problem. These perfectly periodic orbits, referred to as “halo” orbits, do not exist in a full n-body dynamical system such as the solar system. However, quasi‐periodic (i.e. bounded but not precisely repeating) Lissajous orbits do exist in the n-body system. These quasi-periodic orbits are what all libration point missions to date have used. Although they are not perfectly stable, a relatively modest effort at station‐keeping can allow a spacecraft to stay in a desired Lissajous orbit for an extended period of time. It also turns out that, at least in the case of Sun–Earth L1 missions, it is actually preferable to place the spacecraft in a large amplitude (100,000–200,000 km) Lissajous orbit instead of having it sit at the libration point, since this keeps the spacecraft off of the direct Sun–Earth line and thereby reduces the impacts of solar interference on the Earth–spacecraft communications links. Another interesting and useful property of the collinear libration points and their associated Lissajous orbits is that they serve as “gateways” to control the chaotic trajectories of the Interplanetary Transport Network.
In contrast to the collinear libration points, the triangular points (L4 and L5) are stable equilibria (cf. attractor), provided the ratio of the masses M1/M2 is > 24.96. This is the case for the Sun/Earth and Earth/Moon systems, though by a smaller margin in the latter. When a body at these points is perturbed, it moves away from the point, but the Coriolis effect then acts, and bends the object’s path into a stable, kidney bean‐shaped orbit around the point (as seen in the rotating frame of reference).