Cosmology
\ Cosmology of Genetology \ CG \ 1
Fourth quire of a larger publication about Genetology, November 2010
Size: 100 x 70 cm (poster) 50 x 70 cm (folded)
Published by CBK Rotterdam
Text: Martin Wen-Yu Lo 羅聞宇
Design: Raf Vancampenhoudt
Editor: Willem Vanden Eynde
Without a doubt, the single most important problem in physics and cosmology today is Dark Matter. Consider after all of the incredible advancements in science and technology in the 20th century, today, a decade into the 21st century, we still do not know what more than 96% of the universe is made of! Not a clue!
How is this possible when we are able to peer through powerful telescopes in spacetime back to the beginning of the universe, almost at the instant of the Big Bang, that we don’t know what constitutes most of the universe? It brings into question our concept of knowledge, the world, reality, our very being. What is this dark universe to which we belong yet without awareness for so long?
And yet, the world is even more marvelous than we can ever imagine. I present here only one of many theories of dark matter that is being studied by scientists today. It is one which I think is the simplest and the most elegant, called the Brans Conjecture, named after the general relativist, Carl Brans, who first conceived this theory in 1991. The Brans Conjecture explains dark matter as a phenomenon created by a topological property of spacetime called exotic smoothness. We shall explain these strange sounding terms shortly, but for now, the point is that there may not be any “real” dark matter at all according to Bran’s theory. Instead, just as Einstein told us that spacetime is curved by gravity, Brans is telling us that another geometric property of spacetime may be a new type of “smoothness”. When viewed from a part of spacetime with ordinary smoothness such as our own, the distant regions of spacetime with exotic smoothness will appear to have extra forces appearing as dark matter and dark energy.
What is smoothness? The Chinese word for smooth consists of two characters: 光滑. 光 means light , empty, free of things that can obstruct. 滑 means slippery, the three dashes on the left is the radical for water, and the character to the right is for “bone”. My interpretation is that the water makes the floor slippery so you can break your bone on it. Mathematically, this concept can be made very precise: something smooth can be locally approximated by flat surfaces, which is the “differential” – a linear approximation which forms the basis for calculus. Hence smooth objects are also known as “differentiable” and the smooth structure on a smooth object is called its “differential structure”.
Since the invention of calculus by Newton and Leibnitz, mathematicians have taken for granted that there is only one kind of “smoothness” or “differential structure” on an object of any dimension. These smooth regular objects are called manifolds, conceived and described first by Riemann in the early 19th century. Ever since Descartes coordinatized space by “Cartesian Coordinates” like the regular grids of vertical Avenues and horizonal Streets used to coordinatize Midtown Manhattan (New Amsterdam), we think of N-dimensional space, called RN, as the set of points each with a lable [x1, x2, … xN] where x1 is the coordinate in the first dimension, x2 is the coordinate for the second, and so on. From this point of view, there really isn’t that much difference between a 3D world coordinatized by [x1, x2, x3] and the 4D world coordinatized by [x1, x2, x3, x4]. You just add another coordinate and everything is more or less the same – or so it seems.
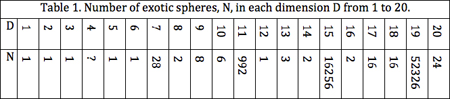
In reality, each dimension is an entirely different beast. Although coordinate-wise all dimensions look the same, [x1, x2, … xN], geometrically every dimension is different in its own way. The situation is so utterly fantastic that even mathematicians themselves had a hard time believing this phenomenon. In 1954, while researching the fabled “Poincaré Conjecture” to characterize the simplest manifold we know, the sphere, John Milnor chanced upon the discovery that S7, the 7-th dimensional sphere, had more than one smooth structure! He called these “exotic spheres”. In fact, there are exactly 28 different smooth structures on S7. More over, it is different in every dimension! The computation of the number of exotic structures in each dimension is very complicated involving Bernoulli numbers.
Now, you will notice from Table 1 that in every dimension from 1 to 20, the number of exotic spheres is known – except in dimension 4, the dimension of spacetime in which we live. This number is the famous “Smooth Poincaré Conjecture in Dimension 4” which is still an open problem. In fact, dimension 4 is truly unique in the context of exotic smoothness.
> In every other dimension, exotic manifolds (high dimensional surfaces) can have only finite numbers of distinct exotic smooth structures. In dimension 4, every known exotic manifold has infinite number of exotic smooth structures.
> In every other dimension, the N-dimensional Euclidean space, RN, given by the set of all coordinates { [x1, x2, … xN], where x1, x2, … xN is a real number}, has only one smooth structure. In dimension 4, RN has an uncountable number of smooth structures.
One cannot help but see that dimension 4 is truly unique in a way which we are still grasping to understand. These facts about exotic smoothness in dimension 4 were only discovered in the 1980’s.
As strange as the ideas of invisible dark matter/energy and exotic smoothness seem to us today, one day in the near future, we will understand what they are and how to manipulate matter, energy, and spacetime with these new concepts. Consider Einstein’s equation E = MC2 and the vast consequences it brought to the world, we cannot but sit up and pay attention when something so fundamental as our knowledge of the nature of matter has been put into doubt! What we think we know best, our material world, is now but a mere shadow of a vast universe we have absolutely no knowledge of. And we can’t even see it! It goes right through us, like phantoms and ghosts. We will turn our attention to the three key aspects in which these concepts touch our lives.
Dark matter cannot be directly observed since they reflect no light thus is completely dark. Hence the only way to detect it at the present is to infer its existence from the way it affects the motion of nearby ordinary matter which we can see. This is how it was discovered. While studying the Coma galaxy cluster in 1933, Fritz Zwicky first noticed that the motion of the cluster indicated there was missing mass in order to account for the faster velocities of the galaxies observed. He coined the term “Dark Matter” for this missing mass. It was not taken seriously at first until in the 1960’s Vera Rubin, using more sensitive instruments, was able to measure the velocities of stars in a galaxy with great precision. She expected stars at a distance further from the center of the galaxy would move slower according to Keplerian orbital theory. To her great surprise, she found all the stars in the galaxy have nearly the same velocties even for stars at the edge of the galaxy where they should move much more slowly. The current accepted theory is that this could only be explained by the existence of dark matter.
When we speak of dark matter and dark energy, there really are two distinct phenomena here. While dark matter is invisible matter in the universe, dark energy is a type of repulsive force causing an accelerated expansion of the universe. From the equivalence of mass and energy from Einstein’s famous equation, dark energy also forms a part of the mass energy of the Universe.
At the moment, exotic smoothness remains a mathematical curiosity without any physical expression or application. However, as we have noted the very unusual multiplicity of exotic manifolds in dimension 4, the dimension of our space-time, suggests that perhaps there are real physical expressions of this phenomenon. At the moment, the problem is that we don’t even know how to work with these exotic manifolds numerically. No one knows how to coordinatize exotic R4, the 4-dimensional Euclidean space, for instance. The standard coordinates [x1, x2, x3, x4] is not smooth for exotic R4’s. So when a 3D fluid is in motion, the 4D simulation object (here time is the 4th dimension) can reach singularities as in turbulence, wave breaking, etc. Is it possible that some of these effects can be described by a change in the smooth structure from the standard smoothness to an exotic smooth structure?
As to the philosophical implications, our species has been in existence on Earth for millennia, yet we are just beginning to discover that the solid real world is not what it seems. It is just 4% of the real Universe. This brings into question our sense of reality, of the solidness of the world, of material things. What is the reality of the other 96% of the Universe which we can neither see nor touch, of which we have absolutely no idea what is involved? What is called into question is not the scientific method which continues to be one of the few lights we have to guide our way around the universe.
What is called into question is the hubris that we now know everything there is to know about the world. What is left unknown is just a few details to clean up our theory. But the Tree of Knowledge is much bigger than we can ever imagine. We see but a small branch and that through a glass dimly. For example, the mathematician Göedel showed that any logical system is incomplete. This great theorem means that if we start out with a set of assumptions (called axioms), there are statements we can make based on these assumptions which can neither be proven to be true or false within these assumption. This means our logic is inherently unable to solve all of our problems. What there is beyond logic is yet to be discovered.
Exotic Smoothness, like Dark Matter, was only discovered in the mid 20th century, a phenomenon which only occurs in dimensions 4 and higher. Whether or not this topological property of spacetime may explain Dark Matter or Dark Energy is not the main point of interest here. What is of interest here is the fact that, like our understanding of the material physical world, our mathematical concept of space is extremely limited by our 3D view of things. The world is a much stranger place than we can ever know or realize.
This should all make us question our materialistic point of view about the nature of reality. We should be more humble and open to other possibilities and other paths to knowledge. But, this is not a call to abandon rationalism or logic in any sense. Reason and logic are the only certain tools we have for dealing with reality. We must use them to discover and climb the other branches of the Tree of Knowledge. As to what these new tools beyond logic might be, I don’t have the slightest idea at the moment. But based on our experience with Dark Matter, our logical system may also represent only a small fraction (maybe 4%?) of various systematic methods to explore and understand the Universe. Intellectually, there may be a transcendental form of reasoning and method of knowing beyond Aristotelian logic yet to be discovered.The knowledge that comes to us through dreams and visions must be understood and interpreted properly. 20th century intelligentsia tended to treat this as inconsequential and bordering on superstitions. Given the waves of rising fundamentalism around the world, this is understandable. But this is a big mistake to think of the non-rational aspects of the psyche as irrational; it is transcendental. What we must achieve is to integrate the two aspects of our mind, the rational with the transcendental to become Whole as Jung would see it.
One person who has come up with an alternate method of knowing is Carl Jung and his theories of the Collective Unconscious and Synchronicity. This brings us to the world of human psyche, spirituality and religion. This also brings us to the world of art because in both these worlds, symbols play a key role. Truth may be expressed in symbolic form through dreams, visions, and art when words and equations are inadequate. As an illustration, I mention Plato’s Symposium where he explains what love is all about in one of the most profound and beautiful stories. Of course, this is not factual. It’s a parable. Surely even in ancient Greece no one believed in this story verbatim. It’s not meant to be factually true. And yet, when you read it, it touches a profound truth within you which delights you heart and makes you say “Oh, yes! That’s how it is. I fall in love when I find and recognize my missing half!” This truth about falling in love is very different from that of the chemistry of attraction and feromones. However, we need both. Neither is complete by itself. It must be integrated.
The knowledge that comes to us through dreams and visions must be understood and interpreted properly. 20th century intelligentsia tended to treat this as inconsequential and bordering on superstitions. Given the waves of rising fundamentalism around the world, this is understandable. But this is a big mistake to think of the non-rational aspects of the psyche as irrational; it is transcendental. What we must achieve is to integrate the two aspects of our mind, the rational with the transcendental to become Whole as Jung would see it.
The ideas about Dark Matter, Dark Energy, and Exotic Smoothness should shock us into realization that Reality is much more profound than the material world we know through our senses alone. We have by no means reached the end of the road so far as our knowledge of what Reality is all about.
Martin Wen-Yu Lo 羅聞宇